Блог SmartyKids представляет материалы по математике для детей. В статье «Площадь круга: как ее найти по формулам» Вы найдете простые объяснения для расчета площади круга по диаметру и другим формулам. Объяснения в статье будут полезны и интересны как для детей, так и для их родителей.
Поиск площади круга – стандартная задача. Обычно, она задается школьникам в шестом классе, помогает мягко перейти к изучению более сложных примеров из тригонометрии.
В этом материале мы расскажем о том, как найти площадь круга с помощью формулы, обратим внимание на основные определения, отличия которых важно понимать учащемуся. Уже через непродолжительное время тренировок, вы сможете полностью освоить все методы решения задач и получать высокие оценки на уроке.
Важные определения
Прежде чем отвечать на вопрос о том, как найти площадь круга
по радиусу или диаметру по формуле, нужно установить основные определения. Мы
будем пользоваться следующими терминами:
- Круг. Так называют замкнутую плоскую кривую, в которой каждая точка имеет равное удаление от центральной.
- Окружность. Это сразу множество точек, которые располагаются на плоскости. При этом расстояние удаления от центра не будет превышать диаметр.
- Радиус. Расстояние от центра круга до любой его противоположной боковой точки.
- Диаметр. Полное расстояние от двух точек, расположенных на равном удалении друг от друга.
Как найти площадь
круга по диаметру: формула
Формула поиска площади для диаметра будет выглядеть так:
S = d2 : 4 × π.
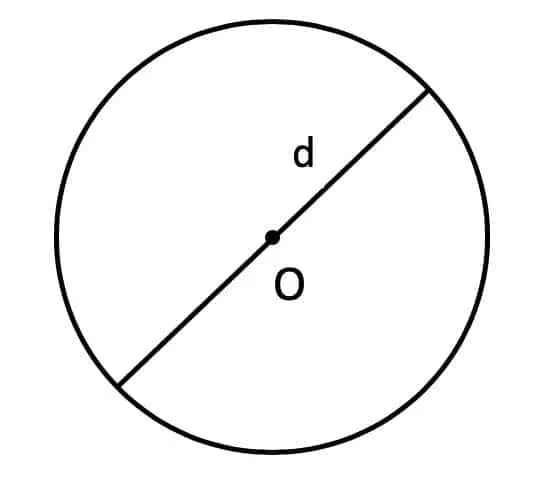
Здесь:
- S – площадь.
- d – диаметр.
- π – константное число, которое в математических расчетах принимается как 3,14.
Как найти площадь
круга по радиусу: формула
Ищем итоговое значение также по формуле. Это S = π × r2. За число π берем константу 3,14. R – это радиус круга.
Как найти площадь через
длину окружности: формула
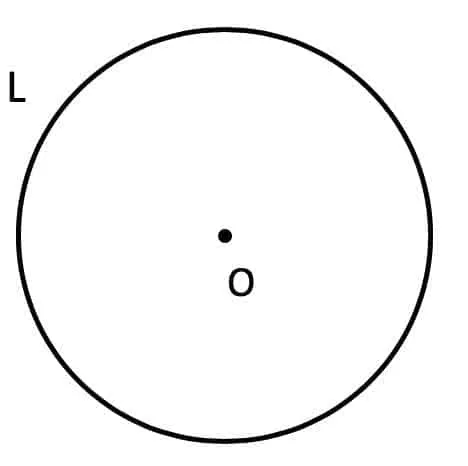
В математике иногда встречаются задачи, в которых известна длина окружности. В таком случае для решения нужно будет использовать стандартную формулу S = L2 : (4 × π).
Здесь L – это и есть площадь окружности.
Как ускорить процесс
обучения: советы специалистов
Есть несколько простых рекомендаций, которые помогают значительно ускорить учебный процесс, помогают быстрее освоиться с тем, как искать площадь круга по разным известным параметрам.
К ним относятся такие, как:
- Убедитесь в том, что ребенок хорошо понимает основные определения. Педагогическая практика показывает, что дети часто путают радиус и диаметр, что приводит к появлению ошибок и выставлению низких оценок учителями.
- В геометрии очень важна наглядность. Все задачи стоит решать исключительно вместе с рисунками круга на бумаге. Это также поможет ребенку значительно быстрее освоиться с использованием циркуля, линейки. Такие навыки сильно помогут в учебе в будущем.
- Не показывайте ученику своего непонимания предмета. Он всегда должен видеть в вас человека, который обладает уверенными знаниями по такому вопросу. Не стоит демотивировать его, рассказывать о бесполезности расчетов.
- Хорошее понимание предмета достигается исключительно через многократное решение задач. Их вы сможете без труда составить своими силами. Все что нужно – ставить условие поиска площади с разными исходными параметрами – длиной окружности, диаметром, радиусом и другими.
- Усложните задачи через введение разных параметров обозначения площади. Есть множество вариантов прописывания площади – это квадратные сантиметры, миллиметры, метры, дециметры и километры. Хорошей математической тренировкой станет перевод разных значений друг в друга. Также можно попробовать посчитать в гектарах. Все это помогает в таких предметах, как геометрия, тригонометрия и математика.
Почему важно
тренироваться в решении задач с площадью круга
Мы рассмотрели, как найти площадь круга по формуле. Осталось
только ответить на вопрос о том, почему понимание этого вопроса представляет
такое большое значение для школьника. Вот лишь несколько важных причин:
- Лучшее понимание геометрических терминов. Их
проще всего освоить на практике. Это пригодится при решении значительно более
сложных задач в старших классах. - Освоение единиц определения площади, решение
примеров по переводу величин друг в друга. Это поможет в геометрии и
математике. Можно воспользоваться умственным счетом или абакусом, что
дополнительно повысит успешность всего учебного процесса. - Создание базиса для решения комплексных
геометрических задач. Они часто направлены на то, чтобы ученик работал с
разными фигурами. При этом если пропустить понимание определения площади,
радиуса и диаметра круга, длины окружности, в будущем могут возникнуть
проблемы, отставание от программы.
Так как в школе дети часто не понимают таких сложных
предметов как геометрия до конца, рекомендуем уделить повышенное внимание
домашним занятиям. Это нужно делать регулярно и системно, но без сильного
давления на школьника, потенциально способного отбить интерес к учебе.
Как определить площадь сечения по диаметру?
Для того чтобы определить площадь сечения по диаметру, нужно использовать формулу для вычисления площади круга. Площадь круга вычисляется по формуле:
S = πr^2,
где S — площадь круга, π — математическая константа, приблизительно равная 3,14, r — радиус круга.
Для того чтобы выразить радиус круга через диаметр, нужно поделить диаметр на 2:
r = d/2,
где d — диаметр круга.
Подставив это выражение для радиуса в формулу для площади круга, получим:
S = π(d/2)^2 = (πd^2)/4.
Таким образом, площадь сечения круга можно вычислить, зная его диаметр, по формуле S = (πd^2)/4. Если диаметр дан в метрах, то площадь сечения будет выражаться в квадратных метрах. Если диаметр дан в сантиметрах, то площадь сечения будет выражаться в квадратных сантиметрах.

Добавить комментарий